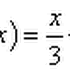Example 1 Sketch the graph of y = (x – 1)2
– 4.
Solution
Now, this is a parabola and
after the next chapter you will be able to quickly graph this without much effort. However, we
haven’t gotten that far yet and so we will need to choose some values of x, plug them
in and compute the y values.
As mentioned earlier, it helps
to have an idea of what this graph is liable to look like when picking values of x. So, don’t
worry at this point why we chose the values that we did. After the next chapter you would also be
able to choose these values of x.
Here is a table of values for
this equation.
x
|
y
|
(x, y)
|
– 2
– 1
0
1
2
3
4
|
5
0
– 3
– 4
– 3
0
5
|
(– 2, 5)
(– 1, 0)
(0, – 3)
(1, – 4)
(2, – 3)
(3, 0)
(4, 5)
|
Let’s verify the first one and
we’ll leave the rest to you to verify. For the first one we simply plug x = – 2 into the equation and compute y.
y = (– 2 – 1)2
– 4
= (– 3)2 – 4
= 9 – 4
= 5
Here is the graph of this
equation.
Example
2 Determine the x-intercepts
and y-intercepts for each of the following equations.
(a) y = x2 + x – 6
(b) y = x2 + 2
(c) y = (x + 1)2
Solution
As verification for each of these
we will also sketch the graph of each function. We will leave the details of the sketching to you to verify. Also, these are all parabolas and as
mentioned earlier we will be looking at these in detail in the next chapter.
(a) y = x2 + x – 6
Let’s first find the y-intercept(s).
Again, we do this by setting x = 0 and solving for y. This is usually the easier of the two. So, let’s find the y-intercept(s).
y = (0)2 + 0 – 6 = – 6
So, there is a single y-intercept:
(0, –6).
The work for the x-intercept(s) is
almost identical except in this case we set y = 0 and solve for x.
Here is that work.
0
= x2 + x – 6
0
= (x + 3)(x – 2) ⇒ x = –3, x = 2
For this equation there are two x-intercepts:
(–3, 0) and (2, 0). Oh, and you do remember how to solve quadratic equations right?
For verification purposes here is
sketch of the graph for this equation.
(b) y = x2 + 2
First, the y-intercepts.
y
= (0)2 + 2 = 2 ⇒ (0, 2)
So, we’ve got a single y-intercepts. Now, the x-intercept(s).
0
= x2 + 2
–
2 = x2 ⇒ x = ±√2 i
Okay, we got complex solutions from this equation. What this means is
that we will not have any x-intercepts. Note that it is perfectly acceptable for this to happen so don’t
worry about it when it does happen.
Here is the graph for this equation.
Sure enough, it doesn’t cross the x-axis.
(c) y = (x + 1)2
Here is the y-intercept work for this equation.
y
= (0 + 1)2 = 1 ⇒ (0, 1)
Now the x-intercept work.
0
= (x + 1)2 = 1 ⇒ x = – 1 (0, 1) ⇒ (– 1, 0)
In this case we have a single x-intercept.
Here is a sketch of the graph for this equation.
Now, notice that in
this case the graph doesn’t actually cross the x-axis at x = -1. This point is still called an x-intercept however.
Labels:
Mathematician
Thanks for reading Graphing – Example. Please share...!