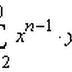Persamaan Kuadrat

Rabu, 18 September 2019

A. Definisi

Persamaan kuadrat adalah suatu persamaan yang variabelnya mempunyai pangkat tertinggi dua.

Bentuk umum : ax²+ bx + c = 0 dengan a ≠ 0, a,b,c ∈ R.

B. Penyelesaian Persamaan Kuadrat

a.      Dengan faktorisasi

Persamaan ax²+ bx + c = 0 diuraikan menjadi (x - x₁)(x - x₂) = 0

b.     Dengan kuadrat sempurna

Persamaan ax²+ bx + c = 0 dibentuk menjadi (px – q)² = r

c.      Dengan rumus ABC

C. Jenis Akar - akar Persamaan Kuadrat

     D = b²  − 4ac

1.      Jika D > 0 maka persamaan kuadrat mempunyai dua akar nyata berlainan

2.      Jika D = 0 maka persamaan kuadrat mempunyai dua akar sama

3.      Jika D < 0 maka persamaan kuadrat mempunyai dua akar imajiner tidak nyata 

4.      Jika D = K² maka persamaan kuadrat mempunyai akar real dan rasioanal.

D. Rumus - rumus Akar Persamaan Kuadrat

    Jika x₁ dan x₂ adalah akar - akar dari ax²+ bx + c = 0, maka berlaku. 

 

 

Beberapa Rumus Praktis

a.      Persamaan kuadrat baru yang akar - akarnya (x₁ ± k) dan (x₂ ± k) dari akar - akar  ax²+ bx + c = 0 adalah

a(x ± k)² + b(x ± k) + c = 0

b.     Persamaan kuadrat baru yang akar - akarnya n kali dari akar - akar ax2+ bx + c = 0 adalah 

ax²+ nbx + n²c = 0

c.      Persamaan kuadrat baru yang akar - akarnya saling berkebalikandengan akar - akar 

ax²+ bx + c = 0 adalah

cx²+ bx + a = 0

d.     Persamaan kuadrat baru yang akar - akarnyadari akar – akar: 

ax²+ bx + c = 0 adalah

ax²+ (b − 2ac)x + c² = 0

e.       Persamaan kuadrat baru yang akar - akarnya salingdari akar – akar ax²+ bx + c = 0 adalah

an².x² + bnx + a = 0

Labels: Matematika

Thanks for reading Persamaan Kuadrat. Please share...!